The FLP theorem

The “FLP” (Fischer-Lynch-Paterson) theorem is a impossibility result about distributed consensus¹, from the 1983 paper Impossibility of Distributed Consensus with One Faulty Process. It says that, under a particular model, a system that can achieve consensus with one node down can’t guarantee that it achieves consensus within any finite time. I’ll explain the core idea of the proof, which is pretty straightforward – most of the details are about formalizing it.

The model is pretty simple: You have some computers, and they can send each other messages. Messages can be reordered/delayed arbitrarily. There’s nothing like a global clock or randomness – computers behave deterministically, and the only source of nondeterminism is how the messages arrive.

We consider possible states of the entire system and the transitions between them. Since computers are deterministic, the only thing that can cause the state of the system to change is a computer receiving a message. When a computer gets a message, it can change its local state and send out new messages in response.

Note that the lack of timeouts means that a computer can’t e.g. send one message and then, if it gets no response within some timeout, recover by sending a different message. If it wants to send a recovery message, it effectively has to send it right away, concurrently with the original message².

We can put all the possible states of the system in a graph, with an arrow from state A to state B if that state transition is possible (i.e. in state A there’s a sent message that, when received, would take the system to state B). The total state of each node in the graph is the internal state of each computer, as well as the set of messages that haven’t yet been received.

Say there are two possible outcomes of the consensus protocol, red and blue. We can color each node of the graph by its outcome: Red or blue if it’s reached consensus, or gray if it hasn’t. The fact that this is a consensus system means that any node reachable from a red node must also be red (and similarly for blue nodes) – once the system has decided on something, it can’t undecide.

Note that a node which can only reach red nodes must itself be red – it might be that no participant knows it yet, but the system has reached consensus if every possible outcome is red.

A graph might look like this (though in most practical consensus algorithms the state space is treated as infinite):

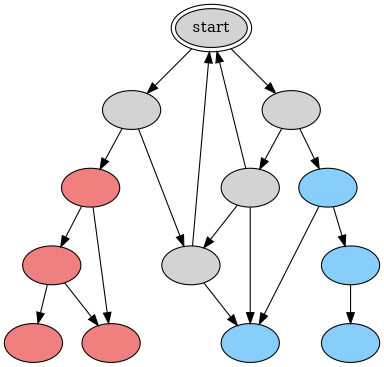
What the theorem is saying is that, for a fault-tolerant consensus protocol, starting at any gray node, there’s always an infinite gray path – at least one way of scheduling messages can prevent you from ever reaching consensus. Equivalently, any gray node has an edge pointing to a gray node.

To show this, consider what it would mean to have a gray node G that doesn’t have a transition to a gray node. This means that all the nodes it points to are either red or blue.

If all the nodes were one color, say red, then G itself would be red. But since G is gray, it must point to at least one blue node as well. So we have something with this shape (there may be other non-gray nodes as well):

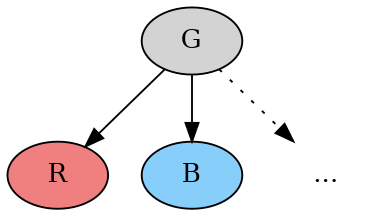
Consider the two transitions from G to R and from G to B.

Every state transition consists of delivering one message (M_r and M_b respectively). There are two possibilities:

1. The two messages are delivered to two different computers.
2. The two messages are delivered to the same computer.

Say it’s case 1. Since the two messages go to two different computers, the overall state they can affect is nonoverlapping. That means delivering both messages is commutative: Regardless of whether we deliver M_r before or after M_b, it has the same effect on the receiving node’s internal state, and causes it to send out the same set of new messages (and similarly for M_b). Therefore they must commute.

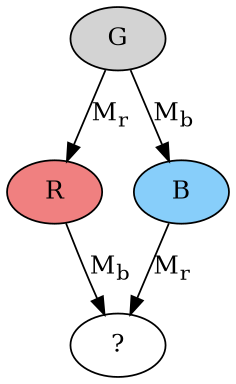
But this is impossible because it would require the node labeled “?” to be both red and blue.

So let’s consider case 2, where the two messages are delivered to the same computer, say C. Since the consensus protocol is fault-tolerant, it must have a way for the system to recover and make progress if C crashes and stops processing messages³.

Since there’s some way for the system to recover if C crashes, there must be at least one message – already inflight, to a computer other than C – that makes the recovery happen (i.e. a way for the system-without-C to make a decision).

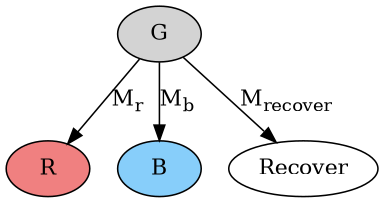
What color is the recovery node? Say it’s red, without loss of generality. But then we have the same situation as possibility 1 above: M_b and M_recover are being delivered to two different computers, so we have the same commutativity problem depending on the order that they’re delivered in.

Either way, the original assumption that G doesn’t have a transition to a gray node leads to a contradiction.

I think it’s worth noting that the asynchronous model is very strong (i.e. significantly constrains what protocols can do). Changing the model allows protocols to avoid this issue. For example, Another Advantage of Free Choice: Completely Asynchronous Agreement Protocols by Michael Ben-Or describes a consensus protocol that can reach consensus with probability 1.

Also, of course, practical systems generally do have some form of clock, and generally a protocol that doesn’t rely on clock drift assumptions for safety can still rely on them for liveness. It’s good to know that liveness is impossible to guarantee formally with minimal assumptions, but we can still treat it as an engineering problem with solutions that work in practice basically all the time.

In practice, this scenario described above shows up as a sort of livelock, e.g. repeated leader elections due to two leaders thinking the other has died. This is a real problem in consensus systems and it’s worth addressing, but the network is rarely adversarial, and often it isn’t a big deal to address in practice.

(Note that the argument for case 2 above is a bit different from the one given in the paper. I think it’s still correct but of course any error is mine.)